Новые математические методы учёных ЮФУ помогут обнаружить развитие онкологии

В рамках совместного исследования Южного федерального университета, Донского государственного технического университета с зарубежными коллегами предложили теорию, которая описывает аномальную (по сравнению со здоровой культурой) структуру раковых эпителиальных слоёв.

С начала прошлого века классические для физики методы и подходы всё чаще используются для описания живых систем. Несмотря на то, что развитие живых организмов контролируется в первую очередь их ДНК, физические и симметрийные законы и принципы продолжают себя проявлять и на этом высоком уровне организации материи. Как продемонстрировал российско-французский коллектив, это справедливо и для плоских клеточных слоев.

«Клетки в плоском эпителии делаться и растут в ограниченном пространстве. Они формируют плотный и прочный, но при этом пластичный слой, защищающий внутреннюю среду организма. Если посмотреть на эпителий сверху, то можно заметить, что каждая клетка представляет собой многоугольник, причём частота появления шести-, пяти-, семиугольников в разных организмах и органах будет примерно одинаковой. В раковом эпителии, для которого характерно неконтролируемое и интенсивное деление клеток, эта закономерность нарушается», — рассказал к.ф.-м.н., Ph.D. Иван Голушко.

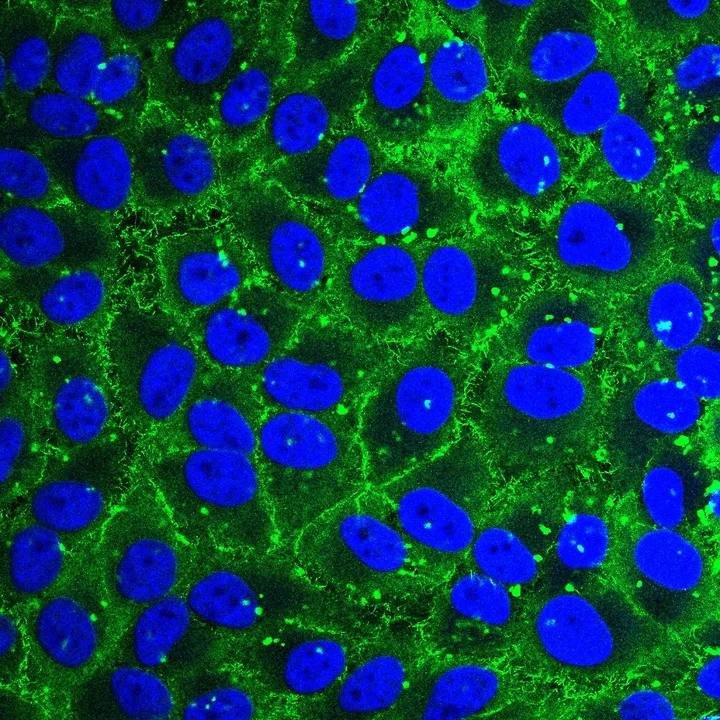
Ростовские учёные проанализировали более 150 фотографий эпителиальных монослоев раковых (HeLa) и здоровых (HCerEpiC) клеток эпителия шейки матки, полученных их французскими коллегами, при этом на каждой фотографии было до 2 тысяч клеток. Для обработки столь большого объёма данных была разработана программа на языке Python, с которой под руководством к.ф.-м.н. Дарьи Рошаль работал самый молодой соавтор – студент физического факультета ЮФУ Кирилл Федоренко.

Определяя границы клеток и анализируя их топологию, учёные обнаружили существенные различия между структурой ракового и здорового эпителия. Клетки здорового эпителия образуют достаточно упорядоченную структуру, состоящую из похожих по размеру и форме многоугольников, около половины из которых – шестиугольники. Исследование показало, что в раковом эпителии такой упорядоченности не наблюдается: популяция содержит много мелких и крупных клеток неправильной, часто удлиненной формы с сильной различающимся числом граней.

Чтобы объяснить такое различие, учёные использовали микромеханическую модель эпителия, рассматривая его как совокупность многоугольников с упругой энергией, и использовали принцип минимизации свободной энергии, отражающий стремление всех физических систем перейти в состояние с наименьшей энергией. Учёные пришли к выводу, что, поскольку раковые клетки делятся примерно в 5–6 раз активнее, система просто не успевает перераспределить энергию и релаксировать в более упорядоченное состояние с большим числом шестиугольников и равномерным распределением клеток по площадям, что и приводит к обнаруженным различиям в топологии клеточных слоев.

Поскольку анализ числа соседей и площадей клеток эпителия достаточно просто автоматизируются, результаты исследования представляют интерес не только с фундаментальной, но и с прикладной точки зрения и могут быть использованы для разработки новых методик диагностики патологий.

«В целом наше исследование предоставляет новые математические инструменты для анализа эпителиального морфогенеза как при раке, так и при нормальном эмбриональном развитии. В дальнейшем мы планируем глубже изучить, как на топологию и «механические» свойства монослоя влияют разнообразные естественные процессы, такие как деление, гибель, рост клеток в рамках более сложных моделей. Мы надеемся, что это позволит объяснить повышение подвижности клеток, наблюдаемое при эпителиально-мезенхимальном переходе и играющее важную роль в совершенно разных процессах от заживления ран до метастазировании», — подытожил д.ф.-м.н., профессор кафедры «Нанотехнология» Физического факультета ЮФУ Сергей Рошаль.

В работу, опубликованную в научном журнале Journal of The Royal Society Interface, вошли результаты исследований по молодёжным проектам, поддержанным Российским научным фондом (РНФ № 20-72-00164) и Российским фондом фундаментальных исследований (РФФИ № 19-32-90134).